오늘은 선택 알고리즘에 대해서 알아봅시다.
선택 문제
선택 알고리즘을 알아보기 전에, 이 알고리즘이 어떻게 나오게 되었는지를 알아봅시다.
그러기 위해서 선택 문제를 우선 설명해야할 것 같은데, 선택 문제란 정렬되지 않은 길이가 n인 수열에서 k번째로 작은 숫자를 찾는 문제를 의미합니다.
통상 이 문제를 해결하기 위한 단순한 알고리즘은 아래의 두가지 일 것입니다.
1. 주어진 수열에서 가장 작은 수를 찾는 과정을 k번 반복했을 때, k번째 작은 수를 찾을 수 있습니다. 선택된 가장 작은 수는 해당 수열에서 삭제하는 방식으로 말이죠.
이렇게 된다면 시간복잡도는 아마 O(kn)이 될 것입니다.
2. 숫자들을 정렬한 이후에, k번째에 위치한 수가 k번째로 작은 수가 될 것입니다.
이는 정렬 알고리즘의 시간복잡도인 O(nlog n)을 따라가게 될 것입니다.
이러한 단순한 방법 외에 우리는 선택 알고리즘을 알아보겠습니다.
선택 알고리즘
선택 알고리즘은 피봇의 개념을 이용합니다. 퀵 정렬과 같은 알고리즘에서 사용되는 개념으로도 우리에게는 익숙하죠.
하나의 피봇을 기준으로 피봇 외의 다른 수들을 피봇에 대한 대소관계를 통해서 좌측과 우측으로 이동하게 되는 과정을 이용할 것입니다.
만약 피봇이 5였고, 7을 비교한다면 7은 5보다 오른쪽으로 가게되고, 2였다면 5보다 왼쪽으로 가는 방식을 이용할 것입니다.
또한 선택 알고리즘은 분할정복을 이용합니다. 분할 정복 알고리즘이란 주어진 문제를 분할하여 해결(정복)하는 방식의 알고리즘이죠.
우리는 피봇을 하나 무작위로 선택하여 피봇을 기준으로 좌우 값들의 분포를 정렬하고, 피봇을 기준으로 몇번째가 찾고싶은지를 통해서 왼쪽 또는 오른쪽을 선택하여 선택 알고리즘을 다시 진행할 수 있습니다.
이러한 방식이므로 우리는 분할정복이라고 할 수 있는 것이죠.
예제를 통해 쉽게 먼저 알아봅시다.
k=7인 수열이 아래와 같이 있다고 해봅시다.

자 이제 무작위로 피봇을 선택하여 해당 피봇을 기준으로 좌, 우 정렬을 진행합니다. 저희는 임의로 인덱스 6에 있는 값을 기준으로 정렬한다고 합시다.
8을 기준으로 정렬을 시작하기에 앞서, 우선 피봇을 0번째 인덱스의 수와 바꿔줍니다.
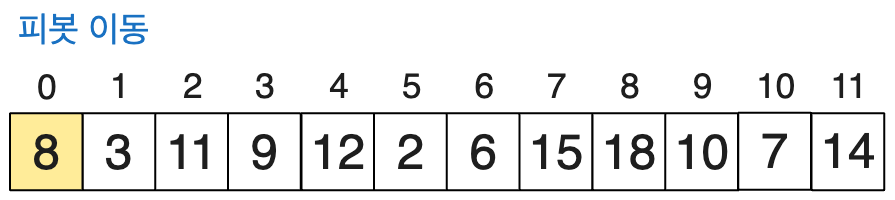
이제, 피봇을 기준으로 모든 수의 정렬을 시작해봅시다. 1부터 11까지 순차적으로 가는 것이 아닌... 1부터 비교하여 우측으로 이동하고, 11부터 비교하여 좌측으로 이동하는 방향으로 진행하겠습니다.
1부터 우측으로 진행할 때는 해당 인덱스의 수가 피봇인 8보다 작은지를 비교하고 작다면 계속 전진, 만약 작지 않다면 멈춥니다. 따라서 1부터 우측으로 진행한 이동 상태는 아래와 같은 그림에서 멈추게 됩니다.

이제 11에서부터 왼쪽으로 이동해봅시다. 14는 통과하겠고 7은 8보다 작게 되니 조건에 맞지 않아 멈추게 될 것입니다. 아래와 같이 되겠네요.
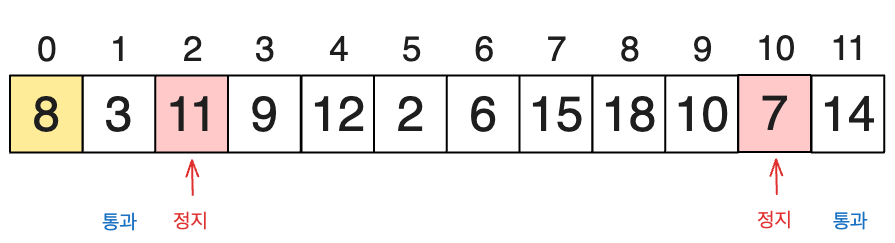
자 이제, 양쪽 모두 정지되었다면, 이 두개의 위치를 바꿔주는 것입니다. 즉, 11과 7의 값을 변경하는 것이죠.
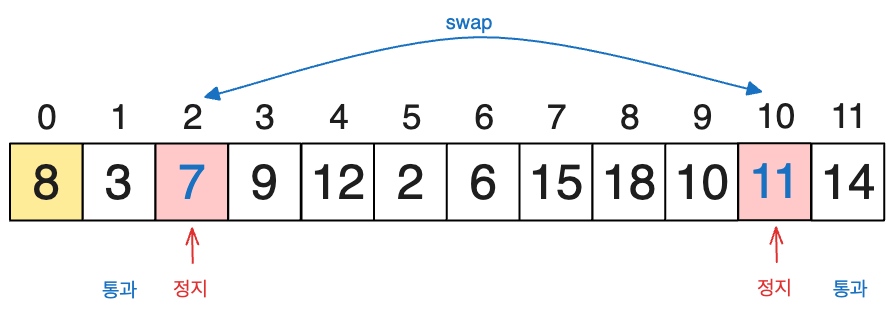
이후, 각자의 순서를 계속 반복합니다. 한번 더 같은 과정을 보여드리자면
우측으로 이동하게 되는 경우는 인덱스 3에서 멈추게 되고,
좌측으로 이동하게 되는 경우에는 인덱스 6에서 멈추게 될 것입니다.
이후 이 둘을 swap하겠네요. 그 결과는 아래와 같습니다.

이를 한번 더 반복하면 4와 5의 인덱스가 서로 swap될 것이고, 비교대상이 서로 엇갈립니다.
좌측에서 우측으로 이동하는 인덱스를 가리키는 변수를 i라고 하고, 우측에서 좌측으로 이동하는 인덱스를 가리키는 변수를 j라고 한다면, 정상적인 과정에서는 i < j 이겠지만, i >= j가 된다면 종료되게 되는 것이죠.
따라서 여기서는 인덱스 4, 5에 swap을 진행하고 i=5, j=4가 되므로 종료하게 됩니다. 그렇게 된 결과는 아래와 같습니다.

이후, 과정은 피봇과 j를 바꿔주는 작업입니다. 즉, 피봇이 정 위치에 들어가서 좌우 정렬 상태를 완성하게 되는 것이죠.
그렇게 되면 아래와 같이 되면서 피봇을 기준으로 좌우가 잘 분류됩니다.

이제 우리가 찾고싶었던 피봇과 비교해봅시다. 우리가 찾고싶은 수가 7번째 수였죠?? 8은 지금 5번째(인덱스 4)니까 우리가 찾고싶은 7번째 수는 8보다 우측에 있겠네요!! 그러니까 우리는 8 기준으로 오른쪽 수열을 가져오게 됩니다.
자! 이제 정말 이 정렬 알고리즘이 분할정복인 이유가 나오게 됩니다.
오른쪽 수열을 통해서 방금 과정을 반복하는 것입니다. 그럼 아래와 같은 수열이 되겠죠.

어?? 근데 조금 달라진 것이 있죠?? 원래 우리는 k=7이어서 7번째로 작은 수를 찾는 것이었는데, 우리가 오른쪽 수열만을 따로 가지고 와서 선택 알고리즘을 진행해야하므로 k는 당연히 달라져야합니다.
k_new = k_old - S - 1을 통해 새로운 k를 구할 수 있습니다. S는 피봇 기준 좌측 수열의 크기가 됩니다.
즉, k = 7-4-1 = 2가 된 셈이죠.
이제 위와 같은 방식으로 수열에서 두번째로 작은 수를 찾으면 됩니다. 그렇게 수행하게 된다면 아마 7번째 작은 수가 10이라는 것을 도출할 수 있을 것입니다.
선택 정렬 vs 선택 알고리즘
선택 정렬과 선택 알고리즘은 엄연히 다른 알고리즘입니다.
선택 정렬은 주어진 무작위 수열을 정렬하는 방법이고, 선택 알고리즘은 선택 문제를 해결하기 위한 알고리즘이 됩니다.
선택 정렬이란?
선택 정렬은 주어진 수열을 오름차순으로 정렬하기 위한 방법으로 총 수열의 길이 n만큼 반복을 진행합니다.
n번의 반복동안 최소인 수열을 찾아 가장 앞에 위치시키고, 이 방식을 진행해나가는 알고리즘입니다.
선택 정렬은 후에 더 자세하게 다루겠습니다.
선택 알고리즘 코드
이제 코드를 통해서 알아봅시다. 우리는 선택 알고리즘을 구현할 때 필요한 파라미터가 무엇인지 먼저 생각해볼 필요가 있습니다.
우선 수열(A)이 필요할 것이고, 해당 수열에서 선택 알고리즘을 진행해야할 시작 인덱스(left)와, 끝 인덱스(right)가 필요할 것입니다. 또한 우리가 찾고싶은 인덱스(k)도 필요하겠죠.
따라서 코드는 아래와 같이 짤 수 있겠습니다.
public static void main(String[] args) {
int[] A = {48, 12, 70, 38, 75, 67, 96, 52, 81};
int k = 5;
System.out.println(k+"번째로 작은 요소: "+selection(A, 0, A.length-1, k));
}
private static int selection(int[] A, int left, int right, int k) {
int p = partition(A, left, right); // p : 좌우 정렬 후 위치한 피봇의 인덱스
int S = (p-1)-left+1; // 좌측 수열의 크기
if(k <= S) // 왼쪽 수열을 선택해서 분할정복을 진행해야할 때
return selection(A, left, p-1, k);
else if(k == S+1) // 원하는 수를 찾았을 때
return A[p];
else // 오른쪽 수열을 선택해서 분할정복을 진행해야할 때
return selection(A, p+1, right, k-S-1);
}
private static int partition(int[] A, int left, int right) {
int i = left+1; // 오른쪽으로 이동하는 인덱스
int j = right; // 왼쪽으로 이동하는 인덱스
int tmp; // swap할 때 이용할 변수
while(i<=j){ // i와 j가 교차되기 전까지
if(A[i] <= A[left]) i++;
else if(A[j] > A[left]) j--;
else{ // swap
tmp = A[i];
A[i++] = A[j];
A[j--] = tmp;
}
}
// 다 진행하면, j와 피봇을 변경한다. 피봇은 left에 있다.
tmp = A[left];
A[left] = A[j];
A[j] = tmp;
return j;
}
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] 그리디 알고리즘 - 허프만 압축 (0) | 2023.11.29 |
|---|---|
| [알고리즘] 분할 정복 - 최근접 점의 쌍 찾기 (1) | 2023.11.28 |
| [알고리즘] 그리디 알고리즘이란? - 1 (1) | 2023.10.17 |
| [알고리즘] Floyd-Warshall 알고리즘이란? (0) | 2023.10.16 |
| [알고리즘] Bellman-Ford 알고리즘이란? (0) | 2023.10.16 |