이번에는 강 연결 성분을 찾는 알고리즘 중 역방향 그래프를 활용하는 Kosaraju 알고리즘에 대해서 알아보겠습니다.
Kosaraju 알고리즘
Kosaraju 알고리즘은 이전 글에서도 잠깐 설명했지만, 역방향 그래프를 통해서 구현합니다.
해당 과정을 그림과 함께 확인해봅시다.

위와 같은 그래프가 있습니다. 가장 먼저 우리는 위상 정렬을 통해서 해당 그래프를 선형으로 정렬하겠습니다.
위상정렬은 어떻게 하냐에 따라 결과라 다르지만, 우리는 3번 정점부터 탐색하기 시작하여
[4, 7, 1, 0, 6, 5, 3, 2, 9, 8]로 정렬했다고 해봅시다.
그럼 이제, 이 위상 정렬을 역순을 취해줍니다.
[8, 9, 2, 3, 5, 6, 0, 1, 7, 4]
그럼 해당 정렬은 위상 정렬의 역순이 되고, 이는 그림 1의 그래프를 역방향 취해준 그래프와 동일하게 됩니다.
아마 그 그래프는 아래와 같을 것입니다.

우리는 이 역방향 그래프와 위상 정렬을 뒤집은 것을 적극 이용합니다.

아래에는 위상정렬 결과와 역방향 그래프가 있습니다. 위상정렬의 가장 첫 원소를 뽑아 해당 정점으로부터 DFS를 시작합니다.
자기 자신을 만날 때까지 진행합니다. 그러면 [2, 8, 9]가 나오게 됩니다.
위 3개의 값들을 정렬 결과인 S에서 제거해줍니다.

그리고 이제 3부터 다시 시작합니다. 3과 연결된 [3, 0, 6]이 나오게 되겠군요.

이제 다시 S에서 제거해줍니다.
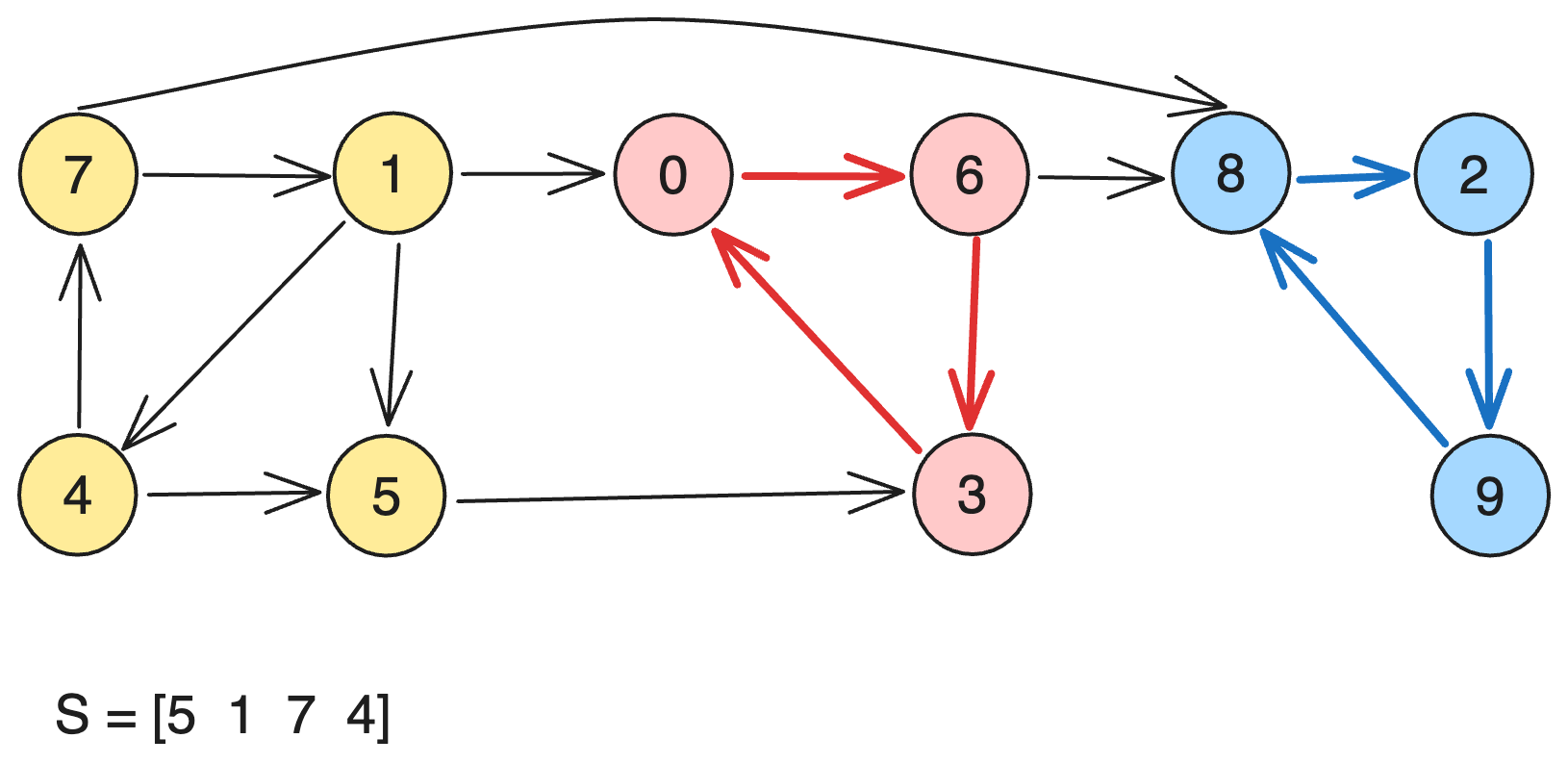
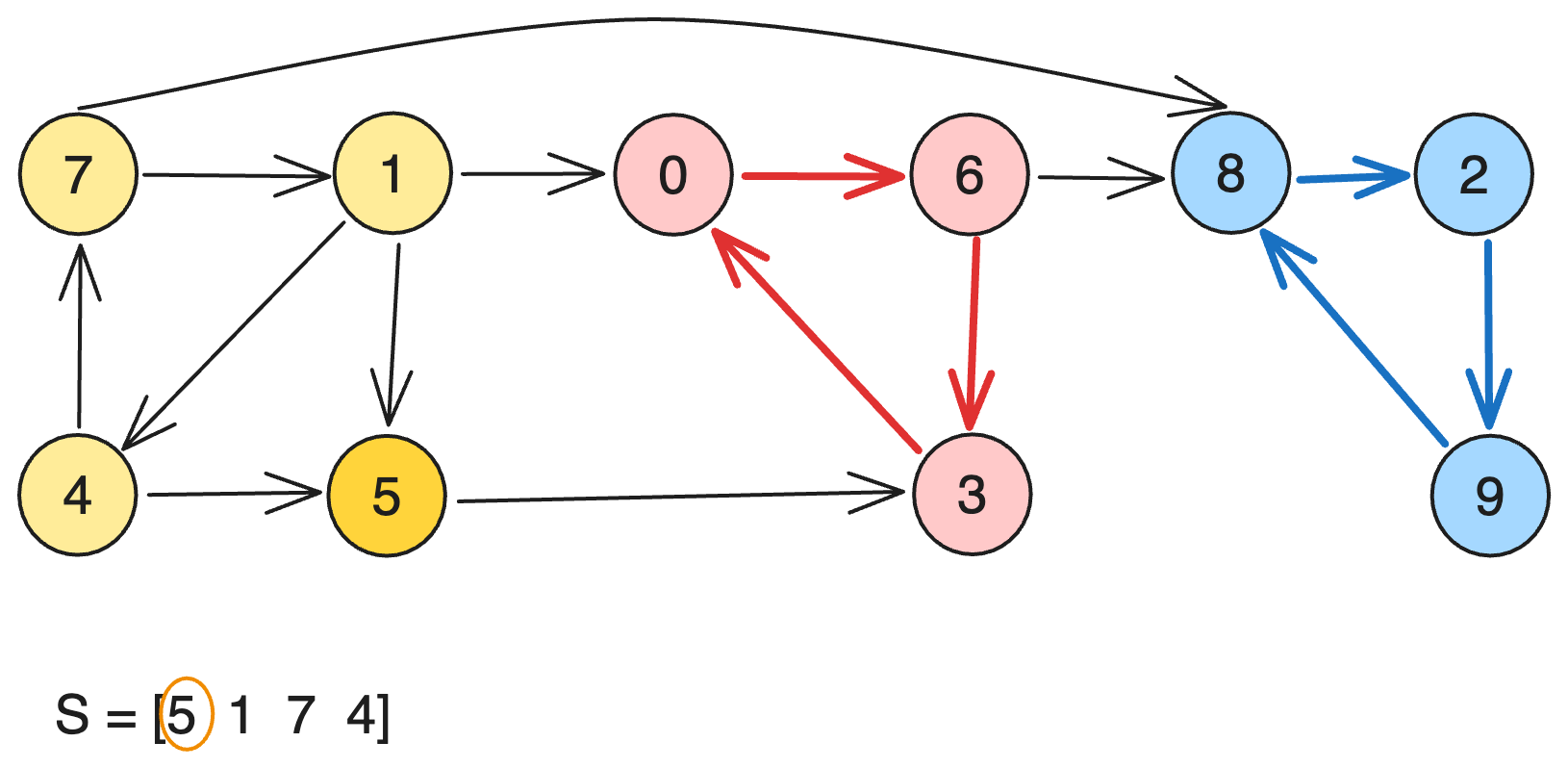
이제 5를 확인해봅시다. 아마 5는 아무도 없이 혼자만 출력되겠군요.
그럼 다음으로 1을 기준으로 DFS하게 되면 [1, 4, 7]이 되면서 종료됩니다.
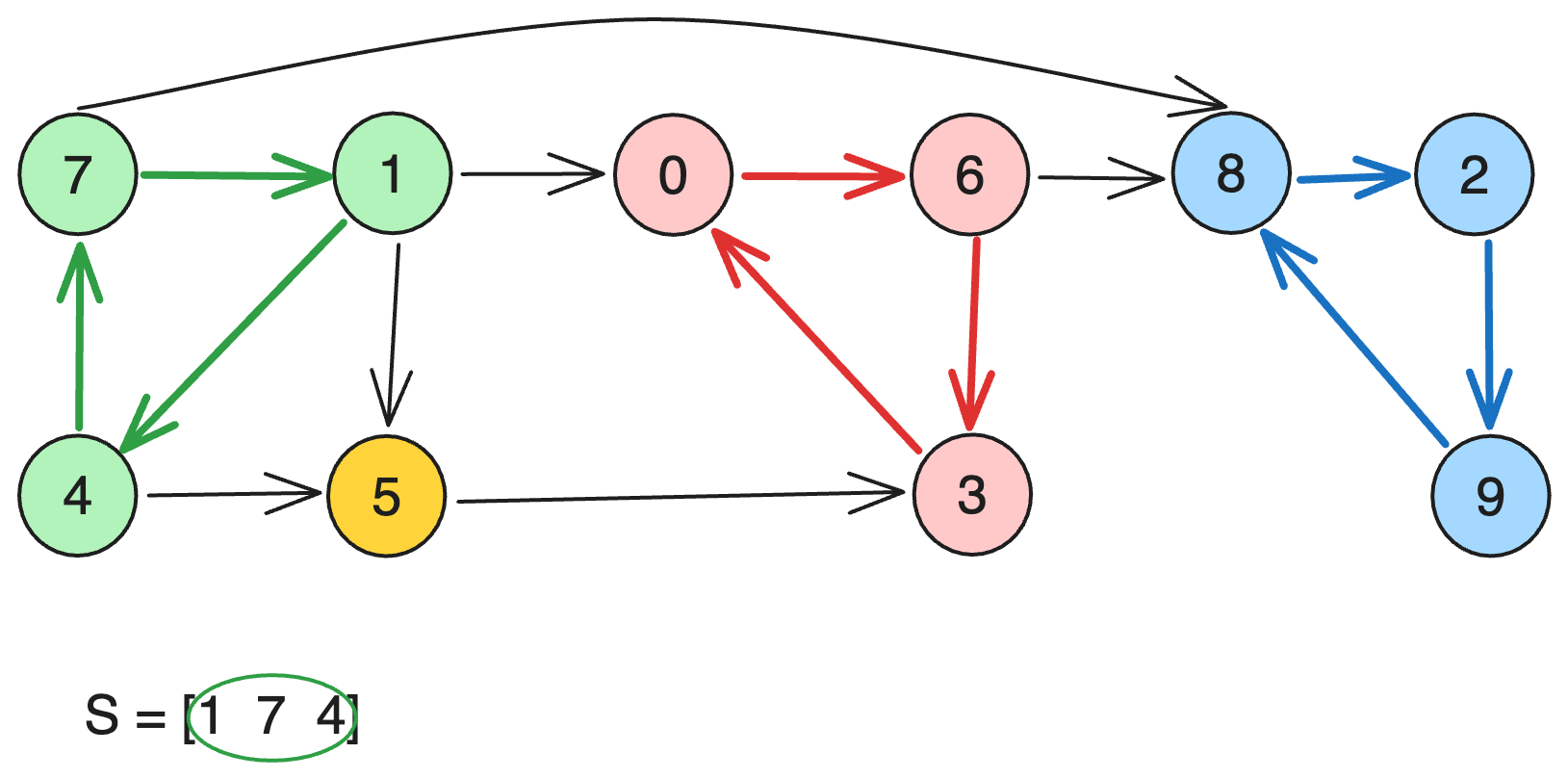
따라서 결국 Kosaraju 알고리즘으로 진행하게 되면 [0, 6, 3], [1, 4, 7], [2, 8, 9], [5]가 되겠군요.
이상으로 Kosaraju에 대한 알고리즘 정리는 마치겠습니다! 사실 코드는 기존 위상 정렬을 이용하는 것과 로직 자체는 간단하기에 첨부하지 않겠습니다. 감사합니다.
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] Kruskal 알고리즘 (1) | 2023.10.15 |
|---|---|
| [알고리즘] Union-Find란? (1) | 2023.10.15 |
| [알고리즘] 강 연결 성분이란? - Tarjan 알고리즘 (1) | 2023.10.14 |
| [알고리즘] 최소 신장 트리란? (0) | 2023.10.14 |
| [알고리즘] 이중 연결 성분이란? (1) | 2023.10.13 |