오늘은 강 연결 성분(Strongly Connected Component)에 대해서 알아보겠습니다.
강 연결 성분(Strongly Connected Component)
강 연결 성분은 방향 그래프에서 연결 성분 내의 임의의 두 정점 u와 v에 대해 u에서 v로 가는 경로가 있고 동시에 v에서 u로 돌아오는 경로가 있는 연결 성분을 의미합니다.
강 연결 성분은 scc라고도 불리며, 이중 연결 성분과 다르게 cut point나 bridge를 포함하지 않습니다.

이러한 그래프가 있다고 해봅시다. 만약 우리가 강 연결 성분을 찾는 알고리즘을 수행한다면 아래와 같은 강 연결 성분을 찾을 수 있습니다.
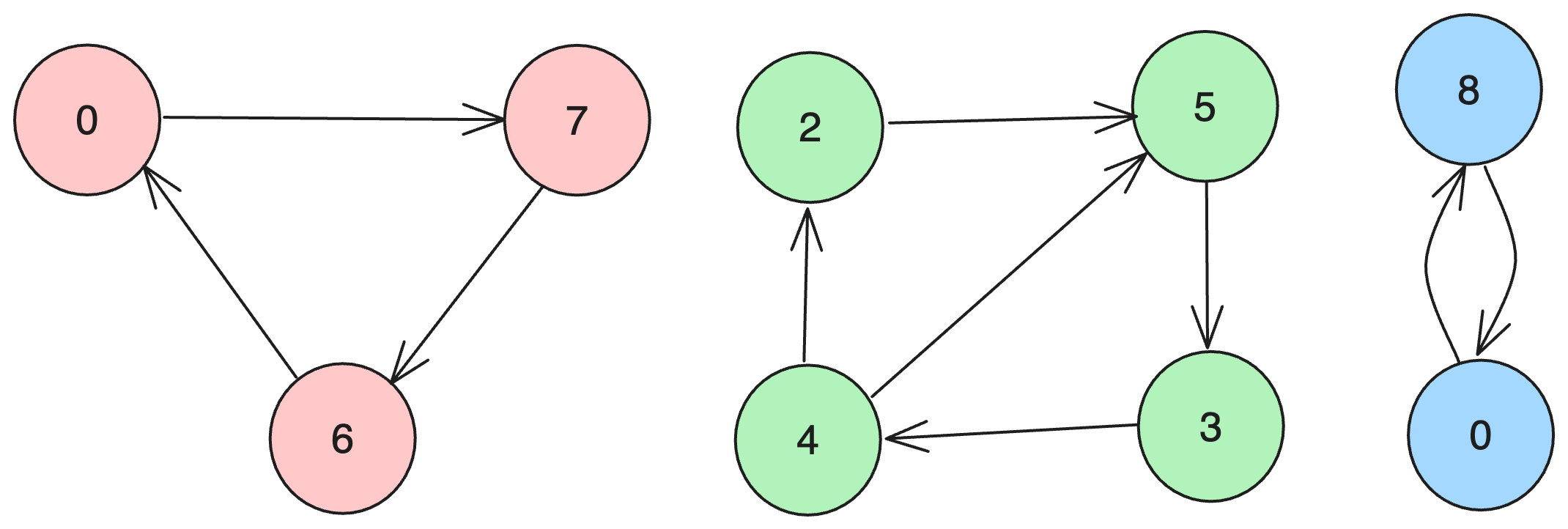
강 연결 성분 알고리즘
scc를 찾기 위한 알고리즘은 대표적으로 2가지가 있습니다.
- 스택을 사용하는 Tarjan 알고리즘
- 역방향 그래프를 사용하는 Kosaraju 알고리즘
저희는 오늘 스택을 사용하는 Tarjan 알고리즘을 이용해서 강 연결 성분을 찾아보겠습니다.
우선 Tarjan 알고리즘의 코드를 확인하기 전에, Tarjan 알고리즘의 흐름에 대해 알고 넘어갑시다.
아래와 같은 그래프가 있다고 해봅시다.

다소 조금 복잡한 그래프로 보이지만, 이 그래프를 0을 기준으로 깊이 우선 신장 트리를 그려보겠습니다.

이와 같은 모습을 보입니다. 여기서 back edge 중 초록색으료 표시한 부분이 있는데, 이는 실제로 방문한 back edge를 의미합니다.
Tarjan 알고리즘은 스택을 이용하여 구현한다고 하였습니다. 우리는 stack을 가지고 이 과정을 함께 가보겠습니다.
가장 먼저 0을 기준으로 DFS를 시작합니다. 우리는 DFS를 하면서 한 가지 특별한 작업을 할겁니다. 바로 나의 부모 vertex를 저장하는 것입니다. 부모 vertex가 갱신되지 않으면 우선 1씩 증가하면서 넣어준 다음, 갱신되는 특별한 경우에 갱신해줄 겁니다.
우선 0을 stack에 넣고 0의 자식 vertex를 방문하게 됩니다. 여기서는 7이 되겠군요.
또한, 자신의 부모를 저장합니다. 별다른 작업을 하지 않았으므로 1이 되겠네요. (부모는 1부터 증가하는 시스템입니다.)

이제 7 차례입니다. 7 또한 stack에 넣고 다음 정점인 1을 방문하게 됩니다.
부모는 2라고 저장하겠네요.

다음 1도 동일합니다. 스택에 1을 넣고, 다음 정점 0을 방문합니다.
부모는 3이라고 저장하겠습니다.

다음 방문할 정점이 0입니다. 0은 이미 방문한 적이 있습니다. 이 때, 1번 정점은 자신의 부모가 사실은 3이 아니라 0이었음을 깨닫습니다. 그렇게 되면 1번 정점은 자신의 부모인 0번 정점이 가지고 있는 값을 복사하여 갖습니다.
따라서 1은 0번 정점과 같은 값인 1을 가질 것입니다.

이제 1번 정점이 가지고 있는 자식은 없습니다. 따라서 DFS를 종료하고 7번 정점에게 갑니다.
7번 정점은 자신의 자식 정점인 1을 보고 판단합니다.
아, 내 부모는 2가 아니라 1의 값을 가지고 있구나
따라서 7번 정점도 자신의 자식과 같은 값인 1을 갖습니다.

이제 7번 정점 또한 DFS를 종료하고 0번 정점으로 갑니다. 0번 정점은 7번 정점을 보고 깨닫습니다.
아 내가 진짜 부모구나
그래서, 자신이 나올 때까지 stack에서 pop을 해줍니다.
그러면 1, 7, 0이 출력될테고 이 셋은 강한 연결 성분을 갖습니다.
Tarjan 알고리즘에 대해서 어느정도 감이 오셨나요??
이제 코드로 확인해보겠습니다.
public static class SCC{
int N;
int[] dfsNum;
int[] lowNum;
int sequence;
List<Integer>[] adjList;
Stack<Integer> stack;
SCC(List<Integer>[] graph){
adjList = graph;
N = graph.length;
}
private void scc(int u) {
sequence = 1;
dfsNum = new int[N];
lowNum = new int[N];
stack = new Stack<>();
int x = existZero();
while(x != -1){
stronglyConnected(x);
// 모든 정점을 방문하기 위해 existZero를 선언합니다.
x = existZero();
}
}
private void stronglyConnected(int u) {
dfsNum[u] = lowNum[u] = sequence++;
stack.push(u);
for (Integer w : adjList[u]) {
if(dfsNum[w] == 0){ // w가 방문 안 된 정점
stronglyConnected(w);
// w가 u의 자식이면 lowNum 갱신
lowNum[u] = Math.min(lowNum[u], lowNum[w]);
}else if((dfsNum[w] < dfsNum[u]) && stack.contains(w)){
// 자신의 자식을 보고 부모를 바로잡는 부분입니다.
lowNum[u] = Math.min(lowNum[u], dfsNum[w]);
}
}
if(lowNum[u] == dfsNum[u]) {
// 자신이 진짜 부모임을 알았을 때, 여기에 들어옵니다.
Integer pop;
do {
pop = stack.pop();
System.out.print(pop + " ");
} while (pop != u); // 자신이 나올때까지 pop
System.out.println();
}
}
private int existZero() {
for(int i=0; i<dfsNum.length; i++){
if(dfsNum[i] == 0)
return i;
}
return -1;
}
}
만약 이 코드를 위 예시의 그래프에 적용한다면 아래와 같은 결과가 나오게 됩니다.

각 줄바꿈은 다른 scc임을 의미합니다. 저희가 직접 찾아낸 1 7 0도 보이네요.
Tarjan 알고리즘의 수행 시간
이 알고리즘은 DFS를 수행해야한다는 점, 결국 최악의 경우 모든 정점과 간선을 확인해야하므로 O(n+m)입니다.
오늘은 scc를 찾는 알고리즘 중 Tarjan 알고리즘에 대해서 알아봤습니다. 다음에는 다른 방법인 Kosaraju에 대해서 알아보겠습니다. 감사합니다.
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] Union-Find란? (1) | 2023.10.15 |
|---|---|
| [알고리즘] 강 연결 성분이란? - Kosaraju 알고리즘 (3) | 2023.10.15 |
| [알고리즘] 최소 신장 트리란? (0) | 2023.10.14 |
| [알고리즘] 이중 연결 성분이란? (1) | 2023.10.13 |
| [알고리즘] 위상정렬이란? (0) | 2023.10.13 |