이번에는 μoperation 중에서 Shift μoperations에 대해서 알아보겠습니다.
기존에 프로그래밍 언어를 배우셨다면, shift 연산에 대해서는 용어 자체가 익숙할 수 있습니다. 어떤 수를 구성하는 비트들을 왼쪽 혹은 오른쪽으로 이동(shift)하는 연산을 의미합니다.
Shift 연산은 Left Shift와 Right Shift로 나뉩니다. 각각에 대해 알아봅시다.
Left Shift
비트를 왼쪽으로 옮기는 연산을 의미합니다. 오른쪽에 빈 자리에는 0으로 채워줍니다. 한 번의 Left Shift는 비트가 수의 표현 범위를 넘지 않는 선에서는 x2를 의미합니다. 아래의 예를 들어 설명합니다. 아래에는 signed magnitude 기법을 사용하여 설명합니다.
2진수로 표현된 0001는 10진수로 1을 의미합니다. 이 수를 left shift 1회를 진행한다면 0010이 되는 것입니다. 단지, 왼쪽으로 한 칸씩 옮기고 오른쪽에 비는 부분에는 0을 채운 것입니다. 0010은 10진수로 2를 의미하고 이는 1의 2배인 값입니다.
하지만 수의 범위를 넘는 경우를 생각해봅시다. 0100은 4를 의미합니다. signed magnituded에서는 4의 2배인 8을 표시할 수 없습니다.(0100에서 0은 sign을 의미하고 나머지 3비트가 수의 크기를 나타내므로, 8을 표현할 수 없습니다.)
따라서 이러한 경우에는 x2를 유지할 수 없습니다.

x << 1은 1만큼 left shift하라는 것을 의미합니다. 위의 글로 설명한 것처럼 0010의 left shift 1의 결과로 우측의 빨간색 비트는 사라지게 되고 파란색 비트가 생성됩니다.
Right Shift
Right Shift는 다소 특별하게 간주해야할 요소가 존재합니다. 따라서, Right Shift는 Logical Shift와 Arithmetic Shift로 또 나뉩니다.
Logical Shift
비트 단위의 shift 연산을 그대로 수행하는 것입니다. 따라서 이러한 shift 연산이 의미있다고 할 수는 없습니다. 이 Logical Shift를 통해서 Right Shift를 수행한다면, 왼쪽에 남는 공간이 생길 것이고 그 부분은 0으로 모두 채워줍니다.

Right Shift를 두 번 수행했다면 위 그림과 같은 것입니다. 파란색 비트는 생성되는 비트이고, 빨간색 비트는 사라지는 비트입니다.
Arithmetic Shift
Shift 연산을 통해서 비트의 이동이 의미있게 하는 방법이라고 생각합니다. 아까 Left Shift를 설명할 때, Left Shift는 수의 범위를 넘지 않는 선에서 비트가 나타내는 수의 x2를 의미한다고 했었죠. 반대로, Right Shift 그 중에서 Arithmetic Right Shift는 ÷2를 의미합니다. 물론 당연히 여기서도 수의 범위를 넘지 않는다는 조건이 있는게 맞긴하지만, 나누기 연산은 수가 작아지지만 0보다 작을 수 없으므로 이러한 규칙을 당연하게 지키면서 수행하게 됩니다.
저희는 Signed Magnitude 기법으로 계속 설명하고 있습니다. 이 Arithmetic Right Shift에서는 Sign bit를 MSB(Most Significant Bit)라고 부릅니다. 우리는 이 shift에서 msb를 빈 자리에 복제하는 방식을 이용할 것입니다.
아래의 예를 보시죠.

Arithmetic Right Shift에서는 MSB를 남는 자리에 그대로 복사합니다. 따라서 이 예시에서 나오는 MSB는 1이므로 빈 자리에 모두 1을 채워넣은 것을 볼 수 있죠.
좌측의 1100은 unsigned magnitude 방식으로 10진수일 때, -4를 의미합니다. 2의 보수를 취해서 확인하면 쉽게 알 수 있습니다.
그렇다면 우측의 1111은 무엇이 될까요?? 이전 설명을 읽으셨다면 -4를 2로 2번 나눠줬으니까, -1이 됩니다. 실제로 -1을 나타내는 것을 알 수 있습니다.
그렇다면 이러한 Shift 연산을 회로로 어떻게 구현했는지 확인해봅시다.
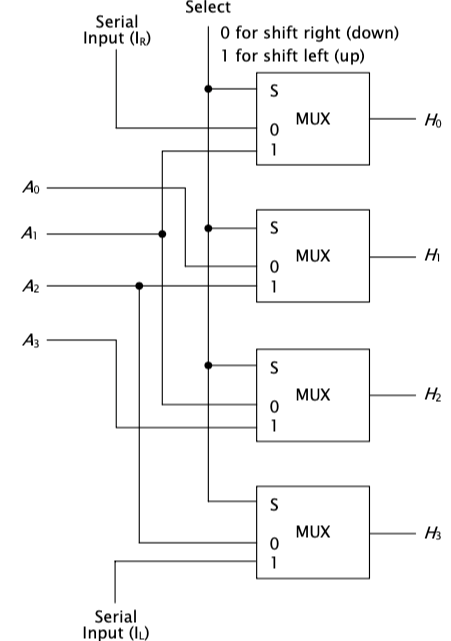
4개의 MUX를 통해서, 구현할 수 있게 됩니다. I_R 과 I_L은 비어있는 비트를 어떻게 채울지에 따라서 결정되는 것입니다. 아래의 표는 위의 회로를 표현하는 진리표입니다.

Arithmetic Logic Shift Unit
지금까지 우리는 Arithmetic, Logic, Shift의 μoperation들을 살펴보았습니다. 이제 이것들을 모두 종합해서 Arithmetic Logic Shift Unit을 구성해보았습니다. 이는 아래와 같습니다.
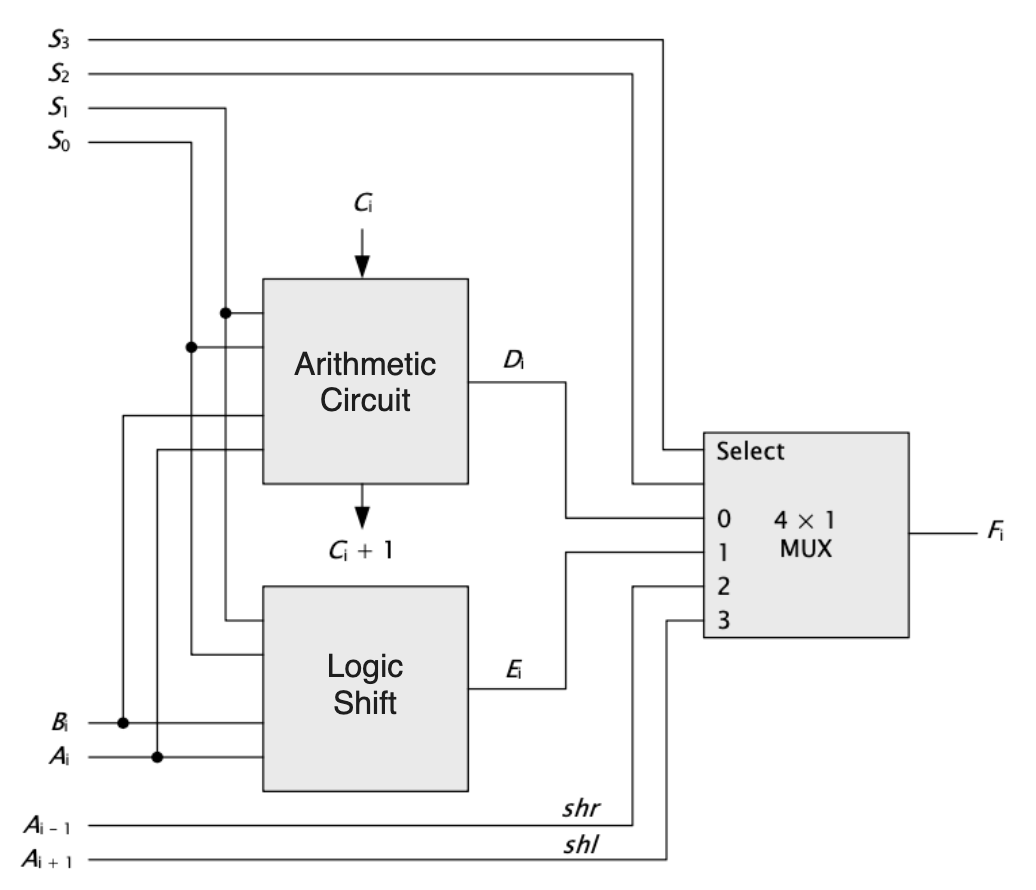
이는 우리가 지금까지 배웠던 모든 μoperation을 가능케하고 그에 대한 진리표는 아래와 같습니다.
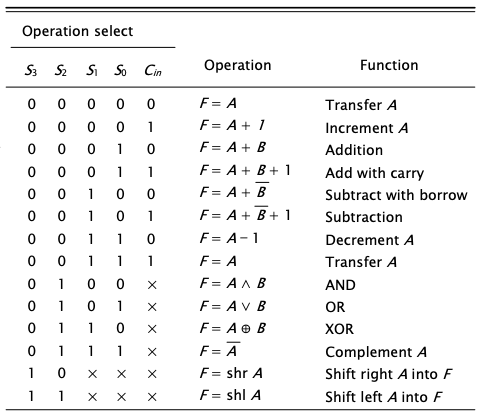
'CS > Computer Architecture' 카테고리의 다른 글
| [컴퓨터구조] 5-2. Computer Instructions (2) | 2023.09.26 |
|---|---|
| [컴퓨터구조] 5-1. Instruction Codes (0) | 2023.09.25 |
| [컴퓨터구조] 4-4. Logic μoperations (0) | 2023.09.24 |
| [컴퓨터구조] 4-3. Arithmetic μoperations (0) | 2023.09.16 |
| [컴퓨터구조] 4-2. Bus and Memory Transfer (0) | 2023.09.14 |