4-1장에서 잠깐 다룬 μoperation에 대해서 조금 더 자세하게 설명한다.
이 책(Computer System Architecture | M. Morris Mano)에서는 μoperation을 4가지로 구분한다. 4-1장에서 다룬 register transfer 그리고 Arithmetic μoperation, Logic μoperation, Shift μoperation.
이번 글에서는 Arithmetic μoperation에 대해서 다룬다.

위에 보이는 것처럼 구분한다. (단, R1 - R2와 R1 + R2' + 1은 같은 의미이다.)
Binary Adder
이러한 Arithmetic μoperation을 구현하기 위해서 Binary Adder가 존재한다. 이 가산기는 n-bit를 더하기 위해 n개의 FA를 사용한다.

나는 논리회로를 듣지 않았기에, FA에 대해서 조금 더 다뤄보자. 빠른 이해를 위해 조금 쉽고 간단하게 설명한다.
FA는 Full Adder의 약자로 전가산기를 의미한다. 두 개의 입력과 이전 값의 carry를 통해서 합(sum)과 carry를 구하는 논리회로를 말한다. 위에 있는 binary adder를 보아도, 두 개의 입력과 이전의 carry가 들어와 C(carry)와 S(sum)이 나옴을 볼 수 있다.
FA와 비슷한 맥락으로 HA(Half Adder)가 있다. 반가산기를 의미하여, 이는 두 개의 입력으로 sum과 carry를 구할 수 있다.
Binary Adder-Subtractor
이처럼 binary Adder로 구현할 수 있지만 치명적인 단점이 있다. Binary Adder는 마치 직렬연결처럼 가장 우측의 계산이 끝나야 그 다음으로 넘어갈 수 있는 순차적인 형태로 보인다. 따라서, 우리는 이러한 단점을 보완하고자 Binary Adder-Subtractor를 설명한다.

그림처럼 XOR gate를 붙여서 Binary Adder-Subtractor를 만든다. 이름에서도 알 수 있다시피 Binary Adder와 다르게 add 연산뿐만 아니라 subtract 즉 뺄셈도 가능하다. 어떻게 가능할까??
이는 M의 값에 따라 달려있다. 만약 M이 0이라면 입력된 A와 B의 합인 A+B를 나타낸다. 하지만 M이 1일 때는, A+B'+1을 나타낸다.

Binary Incrementer
제일 처음에 우리는 Arithmetic μoperation의 종류에 대해서 기술했었다. 그 중에서, 1 비트를 더하는 연산이 존재한다.
A+1, B+1과 같이 말이다. 아래의 그림을 통해 보자.

반가산기 HA를 통해서, 도식화한 모습이다. 간단한 구조이므로 설명은 생략한다.
Arithmetic Circuit
지금까지 여러 산술 μoperation에 대해서 알아봤다. 그럼 이 모든 연산을 가능하게 하는 회로를 살펴보자.

자세한 설명이 필요할 것 같진 않다. 하단의 진리표를 보고, 확인하고 싶다면 주어진 입력값에 대해서 하나하나 이어나가 출력 결과를 확인해보면 아주 직관적으로 이해될 것이다. (논리회로를 잘 모르는 나도 이렇게 시작했다..)
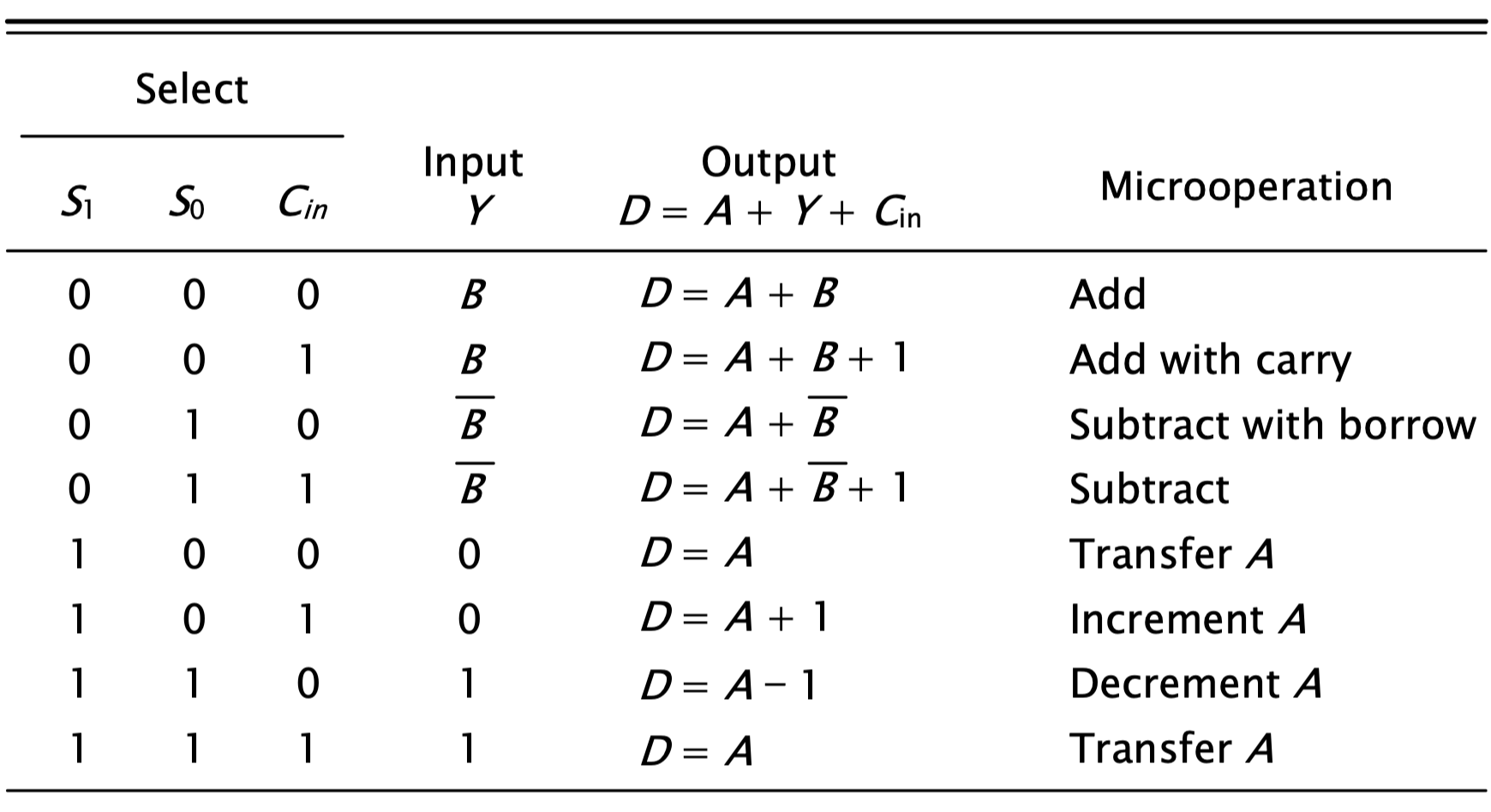
지금까지 산술 마이크로 연산에 대해서 알아봤다. 논리회로를 안 배우고 배우는 컴퓨터구조란 생각보다 학습량이 많아서 걱정했는데, 나름 재미를 붙인 것 같아서 다행이다.
'CS > Computer Architecture' 카테고리의 다른 글
| [컴퓨터구조] 4-5. Shift μoperations (0) | 2023.09.24 |
|---|---|
| [컴퓨터구조] 4-4. Logic μoperations (0) | 2023.09.24 |
| [컴퓨터구조] 4-2. Bus and Memory Transfer (0) | 2023.09.14 |
| [컴퓨터구조] 4-1. Register Transfer (0) | 2023.09.14 |
| [컴퓨터구조] 3-3. Error Detection Codes (0) | 2023.09.13 |