오늘은 이전 글에서 다룬 그래프에 대한 연장선으로 그래프에서 모든 정점을 탐색하는 방법 중 DFS를 다뤄보겠습니다.
DFS란?
DFS는 Depth-First Search의 줄임말로, 깊이를 우선으로 하여 탐색하는 방식을 의미합니다.
하나의 정점으로 시작하여, 그 정점과 이웃한 정점 중 하나를 방문합니다. 방금 방문한 정점에서 다시 이웃한 정점을 확인하고, 이웃한 정점들 중 하나를 방문합니다. 이와 같이 진행하는 방식을 DFS라고 합니다.
아래의 그림으로 확인해봅시다.

위와 같은 그래프가 있다고 가정해봅시다.(사실은 트리라고도 볼 수 있습니다.) 위 트리에서 가장 상위의 정점을 시작으로 DFS를 진행한다면 정점 내에 쓰여진 숫자 순서대로 방문합니다.
DFS의 구현
자바로 구현한 DFS를 확인해보겠습니다.
import java.util.*;
public class Edge{
int adjvertex;
public Edge(int v){
adjvertex = v;
}
}
public class DFS{
int N; // 그래프 정점의 수
List<Edge>[] graph; // 인접 리스트
private boolean[] visited; // 각 노드의 방문 여부
public DFS(List<Edge>[] adjList){
N = adjList.length;
graph = adjList;
visited = new boolean[N];
for(int i=0; i<N; i++){
if(!visited[i]) dfs(i);
}
}
private void dfs(int i){
visited[i] = true; // 방문하면 visited = true;
System.out.print(i+" "); // 방문했다는 것을 출력
for(Edge e : graph[i]){ // 인접한 노드 탐색
if(!visited[e.adjvertex]){
dfs(e.adjvertex); // dfs() 실행
}
}
}
}재귀를 이용하여 DFS를 구현합니다. 인접리스트가 꼭 하나의 연결성분으로 구성되어있음을 보장할 수 없으로 생성자에서 for문을 통해 모든 노드를 탐색합니다.
만약 입력받은 인접리스트가 하나의 연결성분이라면, for문은 한번만 반복하게 됩니다.
이 코드에 대한 수행 과정을 예를 들어 설명해보겠습니다.
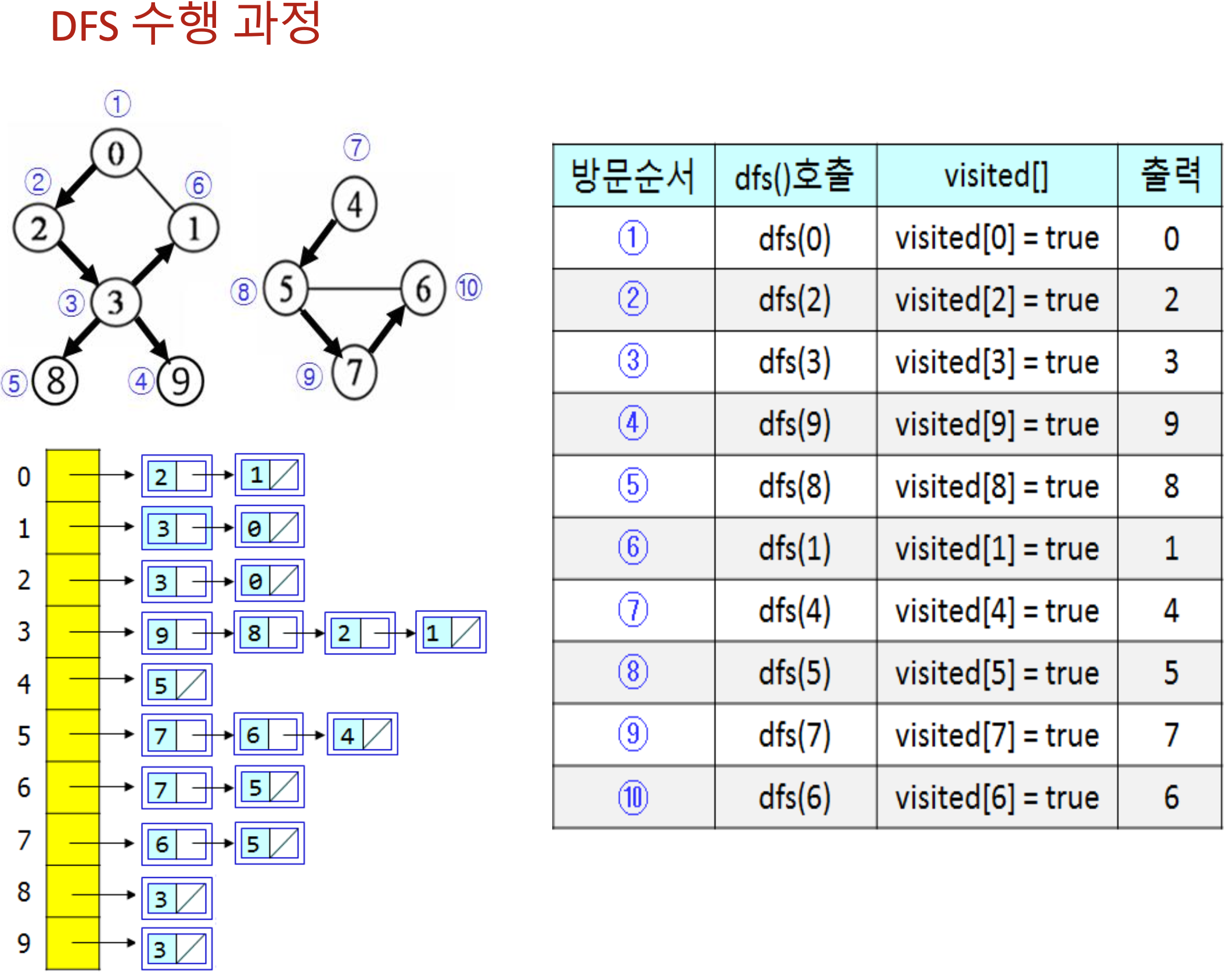
프로그램의 수행 결과는 0 -> 2 -> 3-> 9 -> 8 -> 1 -> 4-> 5 -> 7 -> 6이 되겠습니다.
DFS에 대한 다른 의미를 파악해보겠습니다.
그림 1로 쓰여진 그래프에서 왼쪽의 그래프만 봅시다.

만약 이러한 그래프에서, 이동한 간선만을 살린다면 아래와 같습니다.
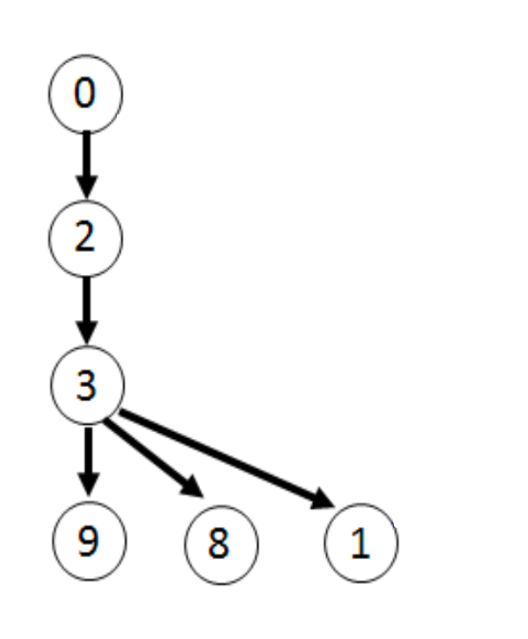
우리는 이전 글에서 신장 트리에 관한 용어를 잠깐 언급했었는데, 특수하게 DFS를 통해서 만들어진 위와 같은 모양을 깊이 우선 신장 트리라고 합니다.
DFS의 수행 시간
DFS의 수행시간은 각 정점을 1번씩 방문하며, 각 간선을 1번씩만 사용하여 탐색하기 때문에 최악의 경우 O(n+m)이고, n은 간선의 개수, m은 정점의 개수입니다.
오늘은 DFS에 대해서 알아봤습니다. 다음 글에서는 비슷하게 그래프를 탐색하는 방법 중 BFS를 다뤄보겠습니다. 감사합니다.
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리란? (0) | 2023.10.14 |
|---|---|
| [알고리즘] 이중 연결 성분이란? (1) | 2023.10.13 |
| [알고리즘] 위상정렬이란? (0) | 2023.10.13 |
| [알고리즘] BFS란? (2) | 2023.10.12 |
| 백트래킹이란? - 백트래킹으로 조합 구현하기 [Java/자바] (0) | 2023.07.18 |