오늘은 정렬방법 중, 위상정렬에 대해서 알아보겠습니다.
위상정렬
위상 정렬(Topological Sort)는 사이클이 없는 방향 그래프에서 정점을 선형 순서로 나열하는 것입니다. 여기서 선형 순서란 일렬로 줄 세우는 것이라고 봐도 되겠습니다.
위상정렬 예제
그럼 위상정렬에 대해서 알아보기 전에!! 왜 위상정렬을 사용하는지, 어떤 경우에 사용하는지에 대해서 알아봅시다.

위와 같은 교과목 체계도가 있다고 해봅시다. 화살표는 선수과목을 의미합니다. 가령, 자료구조는 알고리즘의 선수과목인 것처럼 말이죠.
그런데 여기서 제가 어떤 순서로 들어야할지, 특정 과목부터 시작한다고 하면 무엇을 들을 수 있는지를 위상정렬을 통해서 알아볼 수 있습니다.
만약 위 교과목 체계도에서 위상정렬을 사용한다면, 많은 결과 중 아래와 같은 하나의 선형 순서를 나타낼 수 있습니다.

위상정렬의 구현
위상정렬을 구현하는 방법에는 2가지가 있습니다.
- indegree가 0인 정점으로부터 시작해서 해당 정점을 출력한 후, 제거하는 과정을 반복하는 순방향 방법
- outdegree가 0인 정점을 출력하고 제거하는 과정을 반복하여 얻은 출력 결과를 역순을 취해 얻어지는 결과를 통해 정렬하는 역방향 방법
순방향 방법
순방향 방법은 우리가 지금까지 사용하던 Edge 클래스를 사용하지 않습니다. Node 클래스를 사용하여 구현해야합니다. 이유는, 각자의 노드의 indegree가 몇 개인지 확인하기 위한 필드가 필요하기 때문입니다.
따라서, node클래스는 아래와 같이 구현되어야 합니다.
class Node{
int vertex;
Node nextNode;
}각 노드는 자신의 indegree 개수인 vertex와 다음 노드인 nextNode를 필드로 갖습니다.
그럼 간단하게 예시를 들면서 순방향 방법에 대한 감을 익힌 뒤, 구현해보겠습니다.

이러한 그래프가 있습니다. 각 원 내의 숫자는 노드의 고유 번호이고 괄호 내의 숫자는 indegree 개수입니다.
가장 먼저, indegree가 없는 노드를 선택해야합니다. 여기선 0과 1이므로 어떤 것을 선택해도 무방합니다.
저희는 1번 노드를 선택해보겠습니다. 그렇다면, 해당 노드는 출력 후 삭제될 것입니다.

1번 노드가 출력 후, 사라졌습니다. 따라서 그와 연결된 간선 또한 삭제됩니다.
그러므로, 각 노드의 indegree 개수는 갱신되고, 그 중에서 Indegree가 0인 노드를 찾아봅시다.
0과 3이 있네요, 0을 선택해도 되지만 저희는 3을 선택합니다. 즉, 3을 지웁니다.

이제는 감이 오시나요?? 0 -> 2-> 4 순서대로 지워질 것입니다.
즉, 출력은 1 3 0 2 4 가 될 것입니다.
자!! 이제 이러한 방식을 구현해보겠습니다. 다만, 사실 코드로 구현하기는 순방향보다 역방향이 훨씬 이해하기 쉽고 직관적입니다. 우리는 지금 순방향의 과정을 이해했으니 코드는 의사코드로 대체하도록 하겠습니다.
// graph는 입력 받음
// n은 정점의 개수
for(int i=0; i<n ; i++){
if( 각 정점들이 모두 indegree가 0 이상일 때){
종료! cycle이 있기 때문이다
}
indegree가 없는 vertex 선택.
해당 vertex 출력
해당 vertex와 그 관련된 간선 삭제
}사실 의사코드는 간단하지만, 모든 정점이 0인지를 확인하거나 하는 코드가 역방향보다 복잡합니다.
역방향 방법
역방향 방법은 우리가 outdegree가 없는 노드를 찾는 과정을 Node를 통해서 구현하지 않습니다. 우리에게는 가장 끝에 도달하게 되는 DFS가 있기 때문이죠. 따라서 우리는 DFS를 수행하여 outdegree가 없는 즉, dfs의 재귀가 멈추고 돌아가게되는 시점의 노드부터 먼저 리스트에 추가하고, 해당 리스트를 뒤집습니다.
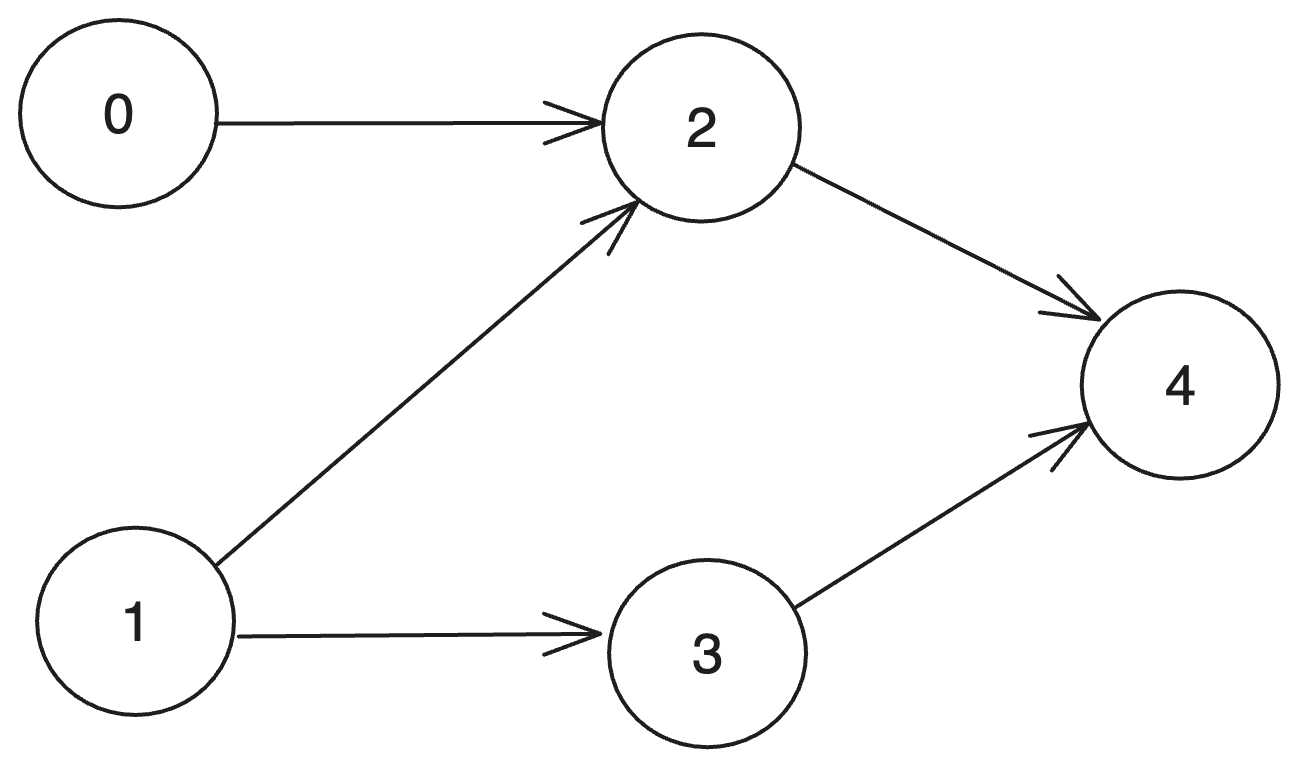
순방향을 설명할 때 썼던 그림입니다. 여기서 첫 시작을 뭐로 해도 상관없지만, DFS와 동일하게 1로 진행해봅시다.
1 -> 2-> 4... 여기서 멈추게 됩니다. 이렇게 재귀 호출을 멈춘다면 리스트에 추가합니다.
즉, 4가 출력됩니다.
DFS에서는 visited를 사용하므로, 굳이 그래프에서 노드를 삭제할 필요가 없어집니다.
4가 출력된 뒤는 2로 돌아가게 되죠. 2에서는 더이상 진행할 노드가 없으므로 2를 출력합니다.
그렇다면 지금은 4 2가 됐습니다.
이제 2를 부른 1로 가서, 1의 나머지 3도 방문해봅시다. 3은 4밖에 없지만 4는 이미 방문했으므로 재귀 호출이 안됩니다.
따라서 3도 출력합니다.
그렇다면 이제 4 2 3이 됩니다.
이와같은 과정을 반복하면
4 2 3 1 0이 되고, 역방향이므로 이를 reverse하게 되면 0, 1, 3, 2, 4가 됩니다.
DFS랑은 다른 탐색 결과가 나오는데 어떻게 된 것일까요?? 실제로 앞서 잠깐 언급했지만 위상정렬이라 함은, 결과가 여러개가 될 수 있음에 주의합니다.
자, 그럼 코드로 먼저 확인해봅시다.
import java.util.*;
public class TopologicalSort{
int N; // 그래프 정점의 수
boolean[] visited; // 노드 방문 여부
List<Integer>[] adjList; // 인접 리스트
List<Integer> sequence; // 위상 정렬 결과
public TopologicalSort(List<Integer>[] graph){
N = graph.length;
visited = new boolean[N];
adjList = graph;
sequence = new ArrayList<>();
}
public List<Integer> tsort(
for(int i=0; i<N; i++) if(!visited[i]) dfs(i);
Collections.reverse(sequence); // 역방향이므로 뒤집습니다.
return sequence;
}
public void dfs(int i){
visited[i] = true;
for(int v : adjList[i]){
if(!visited[i]) dfs(v);
}
sequence.add(i); // 여기는 해당 노드의 outdegree가 없을 때 작동합니다
}
}DFS를 이용하므로 재귀를 사용했음을 알 수 있습니다.
위상정렬의 수행시간
순방향, 역방향 모두 O(n+m)의 시간복잡도를 갖습니다. 여기서 n은 정점의 수, m은 간선의 수를 의미합니다.
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] 최소 신장 트리란? (0) | 2023.10.14 |
|---|---|
| [알고리즘] 이중 연결 성분이란? (1) | 2023.10.13 |
| [알고리즘] BFS란? (2) | 2023.10.12 |
| [알고리즘] DFS란? (0) | 2023.10.12 |
| 백트래킹이란? - 백트래킹으로 조합 구현하기 [Java/자바] (0) | 2023.07.18 |