오늘은 이중 연결 성분에 대해서 알아보겠습니다.
이중 연결 성분이란?
이중 연결 성분이란 무방향 그래프의 연결 성분에서 임의의 두 점 사이에 적어도 두 개의 산순 경로가 존재하는 연결 성분을 의미합니다.
연결성분이란?
그래프에서 정점들이 서로 연결되어 있는 부분을 의미합니다.
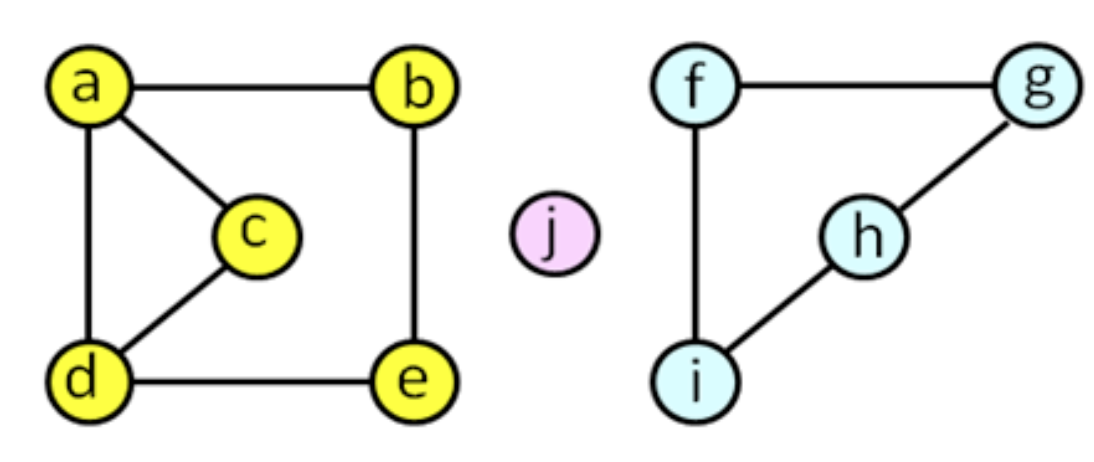
만약 이러한 그래프가 있으면 [a, b, c, d, e], [f, g, h, i], [j]로 연결성분들이 있다고 할 수 있는 것이죠.
그냥 연결되어있는 정점들을 말하는 것이라고 생각하면 됩니다.
이중 연결 성분은 하나의 간선을 삭제하더라도 다른 경로가 존재하므로 연결 성분 내의 정점들의 연결은 유지됩니다.
그렇다면 이중 연결 성분에서 사용되는 용어에 대해 조금 더 자세하 알아봅시다.
단절 정점(Cut Point)
연결 성분의 정점 중 하나의 정점을 삭제했을 때, 두 개 이상의 연결 성분으로 분리될 때의 정점을 의미합니다.
여기서 이중 연결 성분과 연결 성분을 정확히 구분해야합니다.

만약 이런 그래프가 있다고 해봅시다. 이렇게 된다면, 이 그래프 하나가 연결성분이 됩니다.
또한, [0, 1, 2, 3], [3, 5], [4, 5, 6]은 이중 연결 성분입니다. ([3, 5]가 이중 연결 성분인 이유는 아래에서 설명합니다.)
만약 여기서 정점 3이나 5를 삭제하게 된다면 이 하나의 연결 성분이 두 개의 연결 성분으로 나뉘어지게 되므로, 정점 3과 5를 단절 정점이라고 합니다.
다리 간선(Bridge)
어떤 간선을 제거했을 때, 두 개 이상의 연결 성분으로 분리된다면 그 간선을 다리 간선이라고 합니다.
즉, 아래의 그림에서 빨간색으로 표시된 간선이 다리간선이 됩니다.

여기서 한가지 꼭 명심해야할 것은, 다리 간선은 그 자체로 하나의 이중 연결 성분으로 간주합니다. 따라서 이중연결성분 중 하나가 [3, 5]가 되는 것이죠.
이중 연결 성분의 구현
우리는 이제 그래프에서 이중 연결 성분을 찾아야합니다. 그러기 위해서는 cut point를 찾아야합니다.
위에서도 알겠지만, 이중 연결 성분은 cut point에 의해서 나눠지기 때문이죠.
그렇다면 우리는 먼저! 각 정점이 cut point가 되기 위한 조건을 먼저 파악해봅시다.
정점 v가 cut point가 되기 위한 조건
- w가 v의 자식 노드이다.
- w를 포함한 v의 자손 노드와 v를 포함하지 않는 조상 노드를 연결하는 back edge가 없다.
이 두가지 조건을 만족하는 v와 w가 존재할 경우, v는 cut point가 됩니다.
이 조건에 대한 증명을 조금 더 자세하게 다뤄보겠습니다.
사실 어렵지 않으므로 빠르게 설명해보겠습니다.
cut point란 해당 정점를 삭제했을 때, 두 개의 연결 성분으로 나누어질 때 해당 정점를 cut point라고 한다고 했습니다.
만약, 위의 정점 v를 삭제한다고 해봅시다. 그러면 정점 v의 후손 정점들은 정점 v의 조상으로 연결되는 간선이 없으므로 나누어지게 됩니다.
따라서, 이렇게 되면 두 개의 연결 성분으로 나누어지게 되고 이러한 조건이 cut point의 조건임을 알게 되었습니다.
엄연한 증명법은 아니지만, 이정도로 이해하고 넘어가도 충분합니다.
조금 예를 들어서 다시 확인해봅시다.

위 그림은 제일 처음 나왔던 그림 1 그래프에서 0번 정점을 기준으로 DFS 하였을 때 만들어지는 깊이 우선 신장 트리입니다.
실선 화살표는 실제 DFS가 거친 경로이고, 점선으로 이어져있는 간선은 back edge라고 불립니다. DFS에서 지나지 않은 간선 정도로 이해하면 되겠습니다.
이 그래프에서 우리는 정점 3과 5가 cut point임을 이미 확인했습니다.
이제, 이 cut point의 성질을 통해 실제로 만족하는 지 확인해봅시다.
3번 정점부터 확인해봅시다. 3번 정점에는 2번과 5번의 자식 노드가 있습니다. 정점 2번에서는 정점 3의 조상 노드인(정확히는 부모 노드) 0번으로 향하는 back edge가 존재하므로 cut point의 조건을 만족하지 않습니다.
정점 5번에서는 3번 정점의 조상 노드인 0번 노드로 향하는 back edge가 존재하지 않습니다. 따라서 v=3, w=5일 때 cut point의 성질을 만족하므로 정점 3번은 cut point가 됩니다.
이와 같은 맥락으로 정점 5번도 cut point의 성질을 만족하게 되어 cut point가 됩니다.
그렇다면 이제 cut point도 알았으니 구현을 해봐야겠죠??
우리는 dfsnum[]과 lownum[]을 이용하여 cut point를 찾고 이중 연결 성분을 찾아낼 것입니다.
- dfsnum은 단순히 dfs가 방문하는 순서를 나타냅니다. 1씩 증가하게 됩니다.
- lownum은 자식 정점 중에서 가장 작은 dfsnum을 갖는 값을 의미합니다.
이제 이 두 변수 dfsnum과 lownum의 관계식인 lownum[w] >= dfsNum[v]를 통해서 cut point를 찾습니다. 만약 저 부등식을 만족한다면 자식들의 정점의 값들이 정점 v보다 위의 정점과 연결되지 않았다는 것을 의미하기 때문입니다.
각 간선은 stack에 넣어 관리하고, cut point가 나오면 pop해줍니다.
public class BiConnected {
int[] dfsNum;
int[] lowNum;
int sequence = 1;
List<Integer>[] adjList;
Stack<int[]> stack = new Stack<>();
BiConnected(List<Integer>[] graph){
adjList = graph;
dfsNum = new int[adjList.size()];
lowNum = new int[adjList.size()];
}
void biConnected(int v, int u) {
dfsNum[v] = lowNum[v] = sequence++;
for (Integer w : adjList[v]) {
if (w != u && dfsNum[w] < dfsNum[v])
// w와 u가 순환인지 check
// 우측 조건은 DFS로 내려갈 때는 항상 참
stack.push(new int[]{v, w});
if (dfsNum[w] == 0) { // w를 처음 방문한다면
biConnected(w, v);
lowNum[v] = Math.min(dfsNum[v], dfsNum[w]);
if (lowNum[w] >= dfsNum[v]) { // v는 단절정점
while (true) {
int[] pop = stack.pop();
System.out.print("(" +pop[0]+", ");
System.out.print(pop[1] + ") ");
if (pop[0] == v && pop[1] == w)
break;
}
System.out.println();
}
} else if (w != u) // (v, w)가 back edge면
lowNum[v] = Math.min(lowNum[v], dfsNum[w]);
}
}
}
위 코드를 그림 1에 적용 후 실행시키면 아래와 같은 실행 결과를 얻습니다.

저희가 생각한 것과 동일한 결과를 얻을 수 있었습니다.
이중 연결 성분 탐색의 수행 시간
이중 연결 성분은 DFS를 사용하고 stack에 push, pop되는 연산이 있지만 이는 덧셈으로 계산하므로 무시되어 결국 O(n+m)이 됩니다.
n은 정점, m은 간선의 개수가 되겠습니다.
지금까지 이중 연결 성분에 대해서 알아봤습니다. 코드가 바로 와닿지는 않는 느낌인데, 구현 또는 계속 반복하면서 이해하면 도움이 될 것 같습니다. 감사합니다.
'CS > Algorithm' 카테고리의 다른 글
| [알고리즘] 강 연결 성분이란? - Tarjan 알고리즘 (1) | 2023.10.14 |
|---|---|
| [알고리즘] 최소 신장 트리란? (0) | 2023.10.14 |
| [알고리즘] 위상정렬이란? (0) | 2023.10.13 |
| [알고리즘] BFS란? (2) | 2023.10.12 |
| [알고리즘] DFS란? (0) | 2023.10.12 |